In this category, we will be posting 3D models of various mathematical surfaces that are either interesting in appearance or can serve to model something useful or interesting.
Basically, you won't find any solid 3D models here, rather 3D surfaces that you can use as initial models for further modeling. We will normally use MathMod software (former K3Dsurf) to create these mathematical surfaces, so if you need some that haven’t been published yet, we recommend that you install the MathMod software and create them yourselves. Because MathMod software exports polygonal mesh 3D models, you will be able to download all 3D models in polygonal mesh file formats. Whether you are offered the NURBS version of a certain 3D mathematical surface or not will depend on the availability of the software with which we can convert the 3D model. We hope that you are satisfied with our mathematical 3D models, and that you will be able to make some nice and practical use of them.
If you need Mathematical 2D patterns, you can find them here: Mathematical 2D patterns
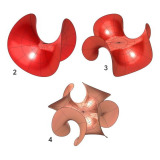
Here you can download one 3D model of the Clifford torus, as well as three 3D models obtained by deleting certain surfaces on it.
This is a 3D model of a Dini surface that is defined in mathematics as a surface with constant negative curvature.
Here you can download 3D models of the Enneper surface, including Enneper surfaces of higher dihedral symmetry (of higher order).
Here you can download 3D models of the following three different mathematical surfaces: helicoid, hyperbolic helicoid, and a surface obtained by transformation of the helicoid into catenoid.
The geometric figure you can download here is called the ‘horn 3D surface’, apparently for the reason that it is very similar to the horns of some animals.
As you can see in the picture, on this page you can download a 3D model of the Klein surface, mostly known by the name ‘Klein bottle’.
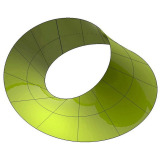
This is a surface 3D model of the Mobius strip (also spelled Moebius, Möbius strip, also band, or loop).
This is a simple 3D model of the surface of a nautilus shell, one of the most known examples of the appearance of mathematical curves in nature.
Here you can download a 3D model of a sphere with a stereographic projection of Cartesian coordinate grid. We called it Stereographic sphere 3D model (Stereosphere 3D model).