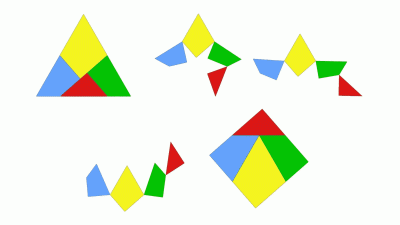
The essence of haberdasher’s problem is how to cut an equilateral triangle into four pieces that could make a square.
Although the Haberdasher's problem is a very interesting geometric task, it is also one quite an interesting puzzle, which can be made quite fast. The Haberdasher’s problem created Henry Dudeney. Haberdasher’s problem dissection puzzle is not one of the difficult puzzles, but its solution is geometrically quite interesting.

127mm (5'') x 110mm (4.33'') x 13mm (0.5'')
If we imagine the pieces hinged together into 3 vertices, all the 4 pieces can be transformed by rotation into either the square or the original triangle.

You can make a haberdasher's problem puzzle according to our cutting diagram, and if you want to make the puzzle with different dimensions, you can easily draw cutting diagram in one of these two ways:
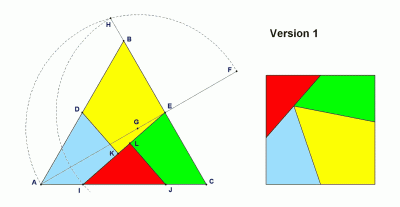
VERSION 1
- Draw an equilateral triangle with points A, B and C
- Bisect AB at D and BC at E.
- Extend AE to F so that EF=EB.
- Bisect AF at G, then, with G as the center, describe the arc AHF.
- Extend EB to H.
- With E as the center, draw the arc HI.
- Make IJ=BE
- Draw line IE
- 9From D and J draw perpendiculars on IE to obtain points K and L.
This way, we made 4 pieces of equilateral triangle that can be rearranged into square.
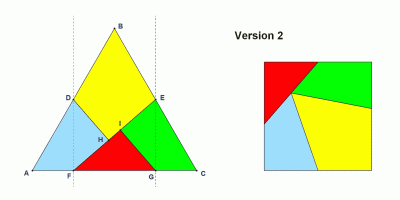
VERSION 2
- Draw an equilateral triangle with points A, B and C
- Bisect AB at D and BC at E.
- Draw the perpendicular lines from D and E on the side AC.
- Determine the intersection points F and G on the side AC
- Draw the line EF.
- Draw the perpendiculars from D and G to this segment and determine the intersection points H and I.